Proof of Goldbach’s Conjecture

Abstract

 

This our Proof of Goldbach’s conjecture’s positive solution (Goldbach was right), is based on the complementary nature between p and q=N–p, with

p+q=N even >=4.

If p and q are both prime numbers, we have a couple of Goldbach for N.

Our simple procedure to find all the G_N couples of Goldbach for a given number N, (an addition table of odd numbers, and the method of columns “a”+“b” have given us the formulas to calculate excactly the number G_N, (real G_N); approximately but more easil (statistical G_N); and therefore to prove the direct proportionality between G_N and N; and this to prove directly the Goldbach’s Conjecture, since G_N>=1 for any even number N, and never G_N=0 (negative solution, its impossibility is proved in our work).

Our formulas for real and statistical G_N are:

(3) G_N=; D_N=; C=wiped out squares with N

(1) G_N~ · 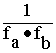for any even N

(2) G₁₀ⁿ~ for N=10ⁿ

At the end of our work, we carry the curve P of prime numbers and the curve G of couples of Goldbach, (G~) for first values of 10ⁿ .

The intermediate values of N between 10ⁿ and 10ⁿ⁺¹ have intermediate values of G_N , between G₁₀ⁿ and G₁₀ⁿ⁺¹.

“ERATOSTENE”

(Francesco Di Noto)

(Annarita Tulumello)

 

 

Dimostrazione della congettura di Goldbach

Riassunto

 

Questa nostra dimostrazione della soluzione positiva del Teorema di Goldbach (costui aveva ragione) si basa sulla complementarità tra p e q=N–p; con

p+q=N pari >=4.

Se p e q sono entrambi numeri primi, abbiamo una coppia di Goldbach per N.

Le nostre semplici procedure per trovare tutte le coppie di Goldbach per un dato N, e cioè G_N (tavola di addizione di tutti i numeri dispari, metodo delle due colonne “a”+“b”) ci hanno fornito le formule per calcolare G_N in modo esatto (G_N reale) o approssimativo (G_N statistico), ma più facilmente e quindi di dimostrare la proporzionalità diretta tra G_N ed N; e con essa anche la soluzione positiva del Teorema di Goldbach, poiché G_N>=1 per qualsiasi numero pari N e mai G_N=0; questo caso comporterebbe la soluzione negativa (la cui impossibilità è pure dimostrata nel nostro lavoro).

Le formule principali per G_N reale e G_N statistico sono:

(3) G_N=; D_N=; C=caselle cancellate

(1) G_N~·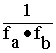=per ogni N pari

(2) G₁₀ⁿ~ per N=10ⁿ

Alla fine del lavoro, riportiamo la curva P dei numeri primi e la curva G delle coppie di Goldbach, tra loro connesse: G~ per i primi valori di N=10ⁿ; valori intermedi di N compresi tra 10ⁿ e 10ⁿ⁺¹, hanno valori di G_N compresi tra G₁₀ⁿ e G₁₀ⁿ⁺¹.

“ERATOSTENE”

(Francesco Di Noto)

(Annarita Tulumello)

 

 

DIMOSTRAZIONE

DELLA CONGETTURA DI GOLDBACH

 

Per questa mia dimostrazione siamo partiti dall’idea fondamentale, mai però venuta in mente a nessuno: una tavola “pitagorica” di addizione di tutti i numeri dispari tranne il numero 1 (non primo) e il numero 2, primo ma non applicabile al Teorema di Goldbach perché, sommato ad un altro primo, darebbe un numero N dispari, mentre Goldbach li voleva pari: N uguale o maggiore di 4 come somma di due primi p e q tali per p+q=N. Cosicché , costruendo questa tavola, avremo un numero N pari ad ogni incrocio tra due numeri dispari qualsiasi: per esempio 20=9+11, 13+17, e così via, come si può vedere nel seguente

 

Reticolo

Si nota facilmente che un certo numero N pari si ripete dal numero dispari N–3 della riga in alto, in diagonale, fino allo stesso numero N–3 della colonna in basso a sinistra; e il numero delle ripetizioni (cioè delle caselle contenenti N) è dato dalla relazione (N–4)/2; per esempio, N=20 parte da 20–3=17 e si ripete in diagonale (20–4)/2=8 volte; esattamente le 8 possibili somme tra numeri dispari da 3 a 17; e tra queste 8 somme di numeri dispari, si annidano le possibili somme di primi che soddisfano il Teorema di Goldbach per N=20.

Come identificarle facilmente, contarle, e per N molto grandi, calcolarne il numero?

È presto detto: cancellando con una linea centrale tutte le righe e le colonne del reticolo che partono da un numero dispari composto (che ovviamente non può fare parte di una coppia di Goldbach) rimangono tutte le caselle in cui il numero N è la somma dei due numeri primi posti all’inizio della riga e della colonna corrispondente; e quindi essi formano una coppia di Goldbach per quel numero N. Nel caso di N=20, tali composti da 3 a 17, sono il 9=3·3, e 15=3·5; per cui si tagliano, come in una sorta di crivello di Eratostene bidimensionale, le due righe e le due colonne che partono da 9 e 15; con ciò si eliminano tutte le coppie miste di primi e di composti che non soddisfano il Teorema, e rimangono solo le caselle agli incroci di righe e colonne che partono dai numeri primi, e che quindi soddisfano il Teorema. La loro somma, infatti, è N.; il reticolo seguente, con i tagli effettuati, rende chiara la procedura: 4 caselle con il numero 20 vengono tagliati e ne rimangono altre 4,

di cui 2 sono speculari alle altre 2, e quindi solo due (3+17), e (7+13) soddisfano il Teorema per N=20.

 

 

Reticolo di soli p+q

(Tutte le somme possibili tra i numeri primi)

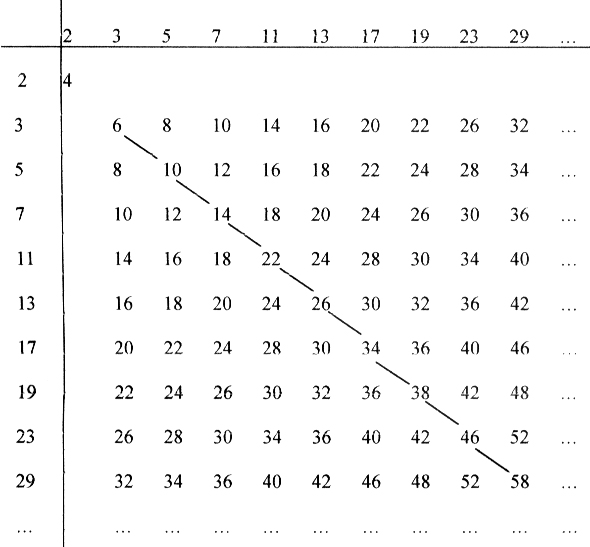Tutti i numeri pari N sono presenti G_N volte in ogni semireticolo, esteso all’infinito; il reticolo è diviso dalla diagonale, che comprende le coppie

p+q=N con p=q=.

Per esempio 6=3+3, 10=5+5, 14=7+7, ecc…; gli altri N sono prossimi alla diagonale, e altri più lontani, a seconda della coppia; quelli della forma N=3+p sono sulla prima riga o sulla prima colonna; i semireticoli sono infatti speculari rispetto alla diagonale.

Rimangono così solo 8 caselle contenenti il N° 20; sono le 4 caselle in cui 20=3+17, 7+13, 13+7, 17+3; ma poiché le ultime due sono simmetriche rispetto alle prime due, e quindi ininfluenti ai fini del Teorema (per il quale 7+13 o 13+7 è uguale) si possono eliminare; rimangono così solo le due coppie 3+17 e 7+13 che soddisfano il Teorema per N=20. Tale procedimento si può estendere all’infinito, cioè per N sempre più grandi, e trovando sempre più coppie di Goldbach al crescere di N.

Il numero di tali coppie è rappresentato dalla lettera G con in basso a destra il valore di N, per esempio, nel caso di N=20, G₂₀=2; G_N è direttamente proporzionale a N, anche per N grandissimi. Questa è una prima prova empirica e positiva del Teorema.

Veniamo quindi ora al calcolo statistico. Ogni diagonale, per ogni N, può scriversi, in altro modo, come due colonne di coppie di numeri dispari “a” e “b”: Sempre per N=20:

 

Tutti i numeri primi sono sottolineati. Quando nella stessa coppia entrambi i numeri sono sottolineati, e quindi primi, ecco che abbiamo una coppia di Goldbach.

Per N=20 sono le stesse coppie, ovviamente, che si desumono dalla tavola di addizione dei primi, e cioè 3+17; 7+13; 13+7; 17+3, in pratica anche qui le prime due, speculari delle seconde. Quindi la metà delle coppie, a partire da N/2, si possono benissimo omettere, come pure la prima coppia e l’ultima, che contengono il numero 1, che non concerne il Teorema (1 non è considerato numero primo). Così abbiamo soltanto (n–4)/4 coppie utili tra le quali cercare le coppie di Goldbach, e che sono esattamente quelle rimaste dopo aver eliminate le coppie nelle quali uno o entrambi i numeri sono composti: e quindi, sempre nel caso di N=20, abbiamo:

 

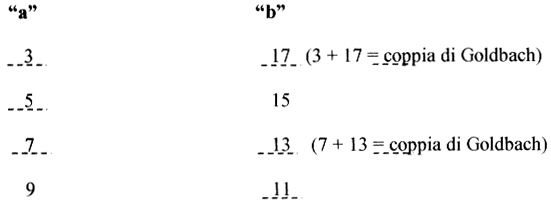Dove, togliendo le coppie 5+15, e 9+11 che contengono i numeri composti 15 e 9, restano le due sole coppie di Goldbach per N=20 e cioè 3+17 e 7+13; per cui per N=20, G₂₀₌2: questo per chiarire la procedura elementare di base.

Per un primo esempio pratico di calcolo (ripetibile poi per qualsiasi altro numero pari N anche molto più grande), consideriamo il numero N=100. Avremo (100–4)/4=24 caselle che contengono il numero 100 nella tavola di addizione di numeri dispari, e anche 24 coppie “a”+“b” con la procedura prima semplificata con il numero 20: dividendo 100–4=96 per 4 otteniamo il numero 24 delle coppie possibili di numeri dispari (le coppie simmetriche sono già state considerate ed eliminate, dividendo 96 per 4 anziché per 2), e cioè 24 coppie utili con le quali calcolare G₁₀₀. Per ottenere tale numero statistico (approssimativo, ma comunque sempre maggiore di 1, e cioè G_N>=1) di coppie che soddisfano il Teorema per N=100, dobbiamo dividere 24 per il prodotto delle frequenze dei numeri primi in entrambe le colonne, considerando che due numeri primi si incontrano sullo stesso punto delle colonne ad ogni multiplo di tale prodotto: dividendo il numero delle coppie, 24 in questo caso, per il prodotto delle frequenze, abbiamo il numero dei loro multipli, dove si incontrano due numeri primi formando così una coppia di Goldbach.

 

Esempio di calcolo delle frequenze del loro prodotto e di G₁₀₀

 

Tabella 2   (p=primo, G=coppia di Goldbach)

Per valori di N anche molto grandi, per esempio di tipo N=10ⁿ , poiché la frequenza tra le due colonne è 2n in entrambe le colonne, e il prodotto delle due frequenze è (2n)·(2n)=4·n² per cui, più semplicemente, per la (1),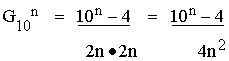

 

 

Per valori molto grandi di n, il –4 del numeratore si potrebbe anche omettere, influendo di una sola unità nel risultato finale, per cui si ha la più pratica e semplice equazione:

(2)

 

 

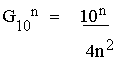
TABELLA: rapporto P/G=2n per valori di N=10ⁿ

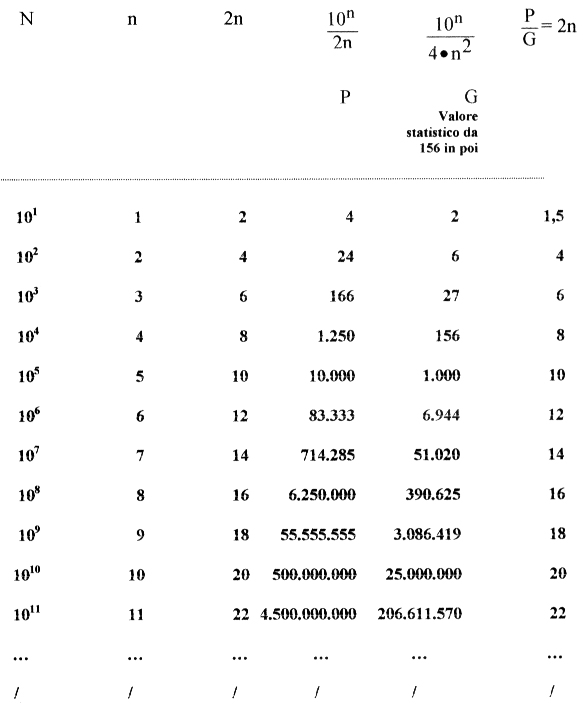Tutto ciò, per qualsiasi N con la (1) e per qualsiasi potenza di 10 con la (2), sarà verificabile con i computer, con appositi software di non difficile preparazione per un bravo programmatore. Poiché G_N è sempre direttamente proporzionale ad N, il Teorema è così dimostrato definitivamente, ed in modo positivo; i timori dei matematici di trovare un numero N per cui il suo G_N=0, sono del tutto infondati; anzi, più grande è N, più grande è il suo G_N (numero di coppie di Goldbach)_.

Per N=10⁹ ; cioè un miliardo, G_N~3.086.419, mentre al buon Goldbach ne sarebbe bastata anche una sola di tutte queste coppie, per ritenere soddisfatto il suo Teorema.

Per valori intermedi tra 10ⁿ e 10ⁿ⁺¹ si hanno naturalmente valori intermedi tra i rispettivi G₁₀ⁿ e G₁₀ⁿ⁺¹ .

Tutti i valori di G_N per tutti gli N costituiscono una curva di coppie simile alla curva dei numeri primi fino ad ogni N; per N=10ⁿ , P=1/2n; la curva di G_N cresce in modo simile alla curva di P (curva dei primi) ma ad un livello più basso.

A questo punto, non ci dovrebbero più essere dubbi sulla validità della nostra dimostrazione positiva del teorema di Goldbach: possiamo anche dimostrare che la soluzione negativa è impossibile. Questa comporterebbe infatti l’uguaglianza numerica tra numeri primi e numeri composti, e la loro perfetta alternanza (in modo analogo ai numeri pari e dispari), in modo che nella tavola di addizione si eliminerebbero tutte le caselle per un dato N, e il suo G sarebbe pertanto uguale a zero, invalidando così il Teorema: ma ciò in realtà non si verifica mai per i numeri primi, la soluzione negativa è quindi impossibile, (vedere la dimostrazione per assurdo) per cui rimane la sola possibilità della soluzione positiva, esposta in questo lavoro e sintetizzata dall’equazione:

(2) G₁₀ⁿ= per i numeri di tipo 10ⁿ

 

(1) e G_N=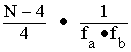

per tutti gli altri N diversi dalle potenze di 10.

P.a. Francesco Di Noto

Prof. Annarita Tulumello

 

 

Dimostrazione per assurdo

 

La formula G_N=

 

in un solo caso, ma irreale, darebbe come risultato G_N=O, dimostrando non valido il Teorema di Goldbach; e cioè solo quando, per un dato N, il numero dei numeri primi fosse uguale a quello dei composti, e fossero perfettamente alternati tra loro e quindi in numero uguale sia nella prima metà di N sia nella seconda metà.

Soltanto in tal caso, infatti, tutte le DN= caselle con N sul reticolo saranno eliminate dai composti, e quindi

 

C=Caselle cancellate dai composti

 

Ma poiché il numero dei primi e quello dei composti fino a N non sono mai uguali tra loro, e inoltre non sono nemmeno perfettamente alternati, il numero C delle caselle con N, cancellate dai composti nel reticolo, sarà sempre inferiore a DN, e quindi la formula  sarà sempre uguale a 1 (per i numeri N più piccoli, e maggiori di 1 per gli N più grandi, in modo proporzionale a N).

 

Esempio di reticolo immaginario con p e c uguali come numero e perfettamente alternati:

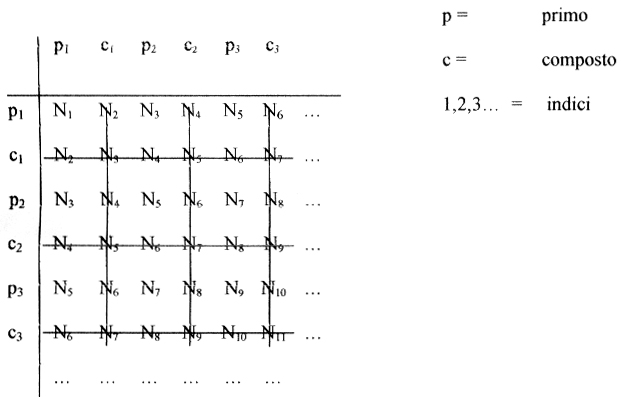Per tutti gli N_2n tutte le caselle con gli N_2n, cioè con indice pari, verrebbero cancellate dai composti c₁, c₂, c₃ (mentre per gli N1,3,5, con indice dispari, cioè N_2n–1, ne vengono cancellate solo la metà) e quindi per gli N_2n, =0

Però, per la diversità (p_i><c_i) tra il numero dei primi e quello dei composti fino a N, e la loro non perfetta alternanza;

 

G_N sarà sempre>=1

 

confermando così la soluzione positiva del Teorema di Goldbach, dimostrato dalla (1) e dalla (2).

 

 

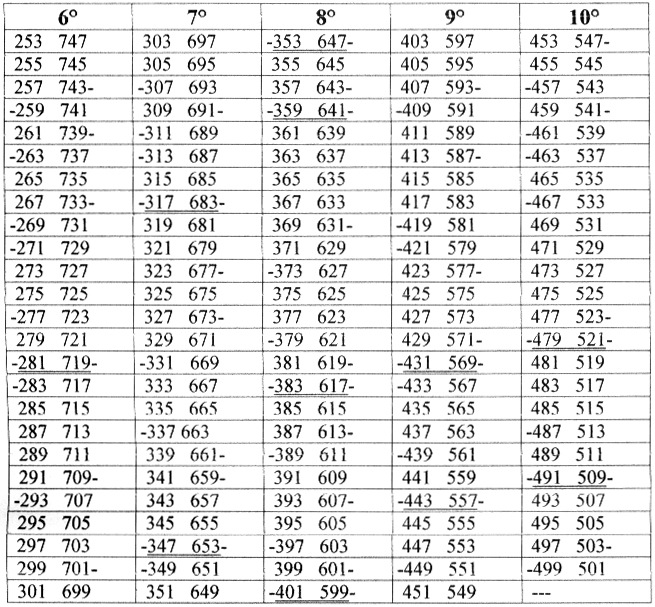
Tabelle di G_N per N=1000 (G₁₀₀₀ stat.=27,7; G₁₀₀₀ reale=27)

con il metodo a+b.

Le 27 coppie di Goldbach sono sottolineate (p+q=1000)

Anche per 1000, (G_N=27, G_N stat.=27,7) oltre che per 100, (G_N=6, G_N stat.=6,25), il calcolo statistico dà quasi lo stesso risultato reale del calcolo col metodo a+b del crivello; mentre per valori più alti di N i due valori G_N statistico, e G_N crivello tendono a non coincidere perfettamente: qualche piccolo scostamento per difetto è pur sempre possibile; G, insomma, è statistico e non deterministico, mentre la verifica con le diagonali o con le colonne a+b dà sempre il valore reale di G_N

Per es. per N=10.000, G statistico=156, G reale=118.

 

P.a. Francesco Di Noto

Prof.ssa Annarita Tulumello

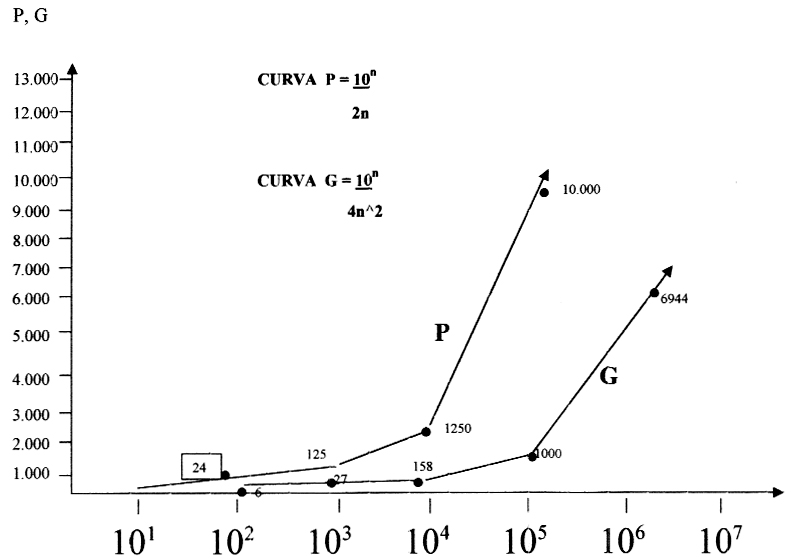P=curva dei numeri primi fino a 10ⁿ
G=curva delle coppie di Goldbach fino a 10ⁿ

 

RICERCA DELLE COPPIE DI GOLDBAC PER
N=104=10.000

In base all’equazione scaturita dalla dimostrazione del Teorema di Goldbach

G_N~G₁₀ⁿ~10ⁿ/(4•n²),

il numero teorico delle coppie di Goldbach per N=10.000 è dato dalla

G₁₀⁴~10⁴/(4•4²) ~ 10.000/64=156,25

il numero reale di coppie di numeri primi che soddisfano il Teorema di Goldbach per N=10.000, trovato con la ricerca manuale col metodo delle colonne a+b, è invece

G₁₀⁴=118,

con uno scostamento s=156–118=38 unità; scostamento, che, seppure notevole, non invalida però la dimostrazione.
Per trovare le 118 coppie di Goldbach per N=10.000, si è proceduto nel solito modo, descritto nella dimostrazione: due colonne “a” e “b” di numeri dispari, “a” da 3 a N/2, e “b” da N/2 a N–3, per un totale di 2500 coppie di numeri dispari, con a+b=N=10.000; tra queste 2500 coppie si trovano le 118 coppie di Goldbach che ci interessano, e cioè di numeri primi p e q tali che

a+b=p+q=10.000 con p e q primi.

Tali colonne iniziano con le coppie:

“a”	“b”
3	9997
5	9995
7	9993
....	....

 

fino alla coppia 4999, 5001; e trascurando le altre 2500 coppie, simmetriche rispetto alle prime 2500, perché darebbero le stesse coppie di Goldbach, ma invertite, il che è irrilevante ai fini del Teorema (7+3=3+7=10 nel caso di N=10).
Ecco di seguito le 118 coppie successive di Goldbach, per N=10.000.
Naturalmente il procedimento è valido per qualsiasi N anche molto più grande; usando i computer con appositi software abbastanza semplici:

colonna “a” con valori da 3 a N/2 (solo numeri dispari 3+2n)
colonna “b” da (N–3)–2n fino a N/2

in modo che ogni elemento di “a” più l’elemento di “b” nella stessa riga, dia N. Le coppie in cui “a” e “b” sono entrambi primi, sono le coppie di Goldbach per il numero pari N.

118 coppie (nell’ordine di successione tra tutte le 2500 coppie di dispari possibili fino a 10.000) di Goldbach per N=10.000 (a+b=10.000)

001. 59+9941		002. 71+9929		003. 113+9887		004. 149+9851
005. 167+9833		006. 197+9803		007. 233+9767		008. 251+9749
009. 257+9743		010. 281+9719		011. 311+9689		012. 449+9551
013. 461+9539		014. 467+9533		015. 503+9497		016. 509+9491
017. 521+9479		018. 553+9437		019. 587+9413		020. 659+9341
021. 677+9323		022. 719+9281		023. 743+9257		024. 761+9239
025. 773+9227		026. 797+9203		027. 827+9173		028. 839+9161
029. 863+9137		030. 941+9059		031. 971+9029		032. 1031+8969
033. 1049+8951		034. 1151+8849		035. 1163+8837		036. 1181+8819
037. 1193+8807		038. 1217+8783		039. 1259+8741		040. 1301+8699
041. 1307+8693		042. 1319+8681		043. 1373+8627		044. 1427+8573
045. 1487+8513		046. 1499+8501		047. 1553+8447		048. 1571+8429
049. 1613+8387		050. 1637+8363		051. 1709+8291		052. 1877+8123
053. 1889+8111		054. 1907+8093		055. 1913+8087		056. 2063+7937
057. 2099+7901		058. 2207+7793		059. 2243+7757		060. 2273+7727
061. 2297+7703		062. 2309+7691		063. 2357+7643		064. 2393+7607
065. 2411+7589		066. 2417+7583		067. 2423+7577		068. 2441+7559
069. 2459+7541		070. 2477+7523		071. 2543+7457		072. 2549+7451
073. 2693+7307		074. 2753+7247		075. 2789+7211		076. 2879+7121
077. 2897+7103		078. 2957+7043		079. 2999+7001		080. 3023+6977
081. 3041+6959		082. 3083+6917		083. 3089+6911		084. 3137+6863
085. 3167+6833		086. 3209+6791		087. 3221+6779		088. 3299+6701
089. 3347+6653		090. 3449+6551		091. 3527+6473		092. 3677+6323
093. 3701+6299		094. 3779+6221		095. 3797+6203		096. 3803+6197
097. 3947+6053		098. 3989+6011		099. 4013+5987		100. 4019+5981
101. 4073+5927		102. 4133+5867		103. 4139+5861		104. 4217+5783
105. 4259+5741		106. 4283+5717		107. 4289+5711		108. 4349+5651
109. 4409+5591		110. 4481+5519		111. 4493+5507		112. 4517+5483
113. 4523+5477		114. 4583+5417		115. 4649+5351		116. 4703+5297
117. 4721+5279		118. 4919+5081